Geht doch. Ihnen sei verziehen

On Topic:
Zitat:
Zitat von MasterOers

aber da verwirrt mich dieser x -> Pfeil völlig.
|
Natürlich verwirrt dich das, denn das ist falsch was in dem Buch steht. Solche Schlampereien in Schulbüchern regen mich maßlos auf.
Sprich ruhig auch deinen Lehrer darauf an und verweise ihn gerne auf diesen Thread.
Eine Funktion ohne die Mengen anzugeben, auf der sie arbeit, ist ein absolutes no go!


Was da gemeint ist war folgendes. Gegeben ist eine Funktion f die (vermutlich) wie folgt definiert ist:

Also eine Funktion einer Veränderlichen definiert auf den reellen Zahlen ohne die Null.
Was man nun möchte ist den Differenzenquotienten bestimmen. Dazu muss man sich klar machen was dieser bedeutet und wie man ihn angibt.
Bedeutung:
Der Differenzenquotient ist die Steigung der Sekante. Eine Sekante schneidet die Funktion in (mindestens) zwei Punkten.
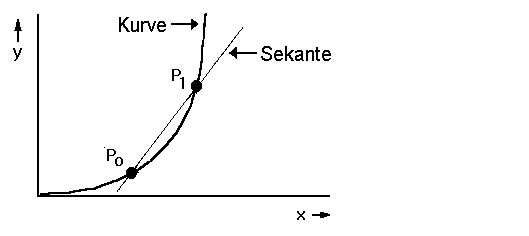
Was das bedeutet solltest du nun aus dem vorherigen Schuljahr wissen, als es um Geraden und deren Steigung ging. Nette Schulmerkregel:
"Hub durch Schub"
Deshalb ergibt sich diese Setigung, 1:1 so wie du das im Schuljahr zuvor gelernt hast, als den Term

Das ist dein bekanntes "Steigungsdreieck". Falls dich der Zähler verwirrt: Das sind "y-Werte" der Bruch ist eben "Hub durch Schub"

Hub, als auch Schub, sprich Zähler und Nenner sind Differenzen von zwei Koordinaten. Du hast also "Strecken" da.
Solch eine "Strecke" hat Anfangs- und Endpunkt. Klar, wenn du eine Linie zeichnest fängst du irgendwo an und hörst irgendwo wieder auf.
Deshalb ist dieser Ausdruck für ein (kompaktes) Intervall I geschrieben, nämlich

Was du also machen musst ist ganz stur einsetzen. Hier passiert noch gar keine "elegante" Mathematik, sondern das ist sowas von gerade aus rechnen. Dein erste Ansatz war der richtige Weg.
Auf ein Wort:
Manchmal schreibt man den Differenzenquotienten in der "h-Darstellung". Diese Darstellung ist zu dieser äquivalent, jedoch ist obige anschaulicher, weil man das Steigungsdreieck wirklich direkt sehen kann, während man einer h-Darstellung das Dreieck nicht intuitiv ansehen kann.
Die Äquivalenz kann man sofort nachrechnen, auch gerade aus. Mache das doch als Übung, wenn du magst.
Nebenbemerkung:
Der tieferliegende Grund für die h-Darstellung ist nettere Schreibarbeit. Eine Ableitung ist eigentlich eine sog. lineare Abbildung. Das ist lineare Algebra. Dort muss man zeigen, dass eine solcher Homomorphismus genau dann existiert, wenn ein Restglied schneller zu Null konvergiert als die Norm im Differenzenquotient. Hier ist es deutlich angenehmer in h-Darstellung zu arbeiten, auch weil man dann andere Notationen sinnvoll einführen kann. Stichwort Landau-Symbole.
Das war für die Schule unwichtig, aber nur damit du weisst was das soll.
Wegen der Äquivalenz rate ich dir aber, nur mit obiger Darstellung zu arbeiten.
Und nun stur einsetzen und ausrechnen


